Tic-Tac-Toe
or how to achieve an optimal strategy with game theory, reinforcement learning... and bunch of matchboxesChapters
- What?!
- Board, groups, symmetries and ternary numbers
- Game theory and minimax theorem
- MENACE or a pile of matchboxes mastering the game
- Reinforcement learning
What?!
Tic-tac-toe or in british english noughts and crosses is an ancient game which every seven years old children learns how to play and not to lose in exactly nine plays or so. Why would you spend your time with playing and studying such a triviality? Well, I got interested in Reinforcement learning recently. So I can use it for some more nasty stuff and tic-tac-toe is a classic example such that even Sutton & Barto [3] don't hesitate to put it into the book's introduction.
As well as many other trendy machine learning techniques were invented in the early 60s [4], so does Reinforcement learning. I was shocked (ok, positively surprised) when I watched one of Hanna Fry's Christmas lectures where Matt Parker came with a pile of matchboxes which could play noughts and crosses. For my surprise it wasn't Matt Parker who invented it, not even in-that-time PhD student Matt Scroggs [5] who he referred in his previous video. It was a former Bletchley Park researcher Donald Michie in 1960 who came up with a smart way how to teach a bunch of matchboxes with beads in it to play noughts and crosses [1, 2].
However, every seven years old children learns how to play and not to lose, it is possible to find and check all possible games, and define perfect unbeatable player which won't lose any game. To do that, we will take a look at game theory approach. [6]
In this article, I try to explain some valuable math properties about the game and try to come up with a few ways how to teach a computer to play tic-tac-toe.
Board, groups, symmetries and ternary numbers
The tic-tac-toe board is a 3 × 3 square-shaped grid. For simplicity and future references, let's denote all the fields by numbers 0-8, where the center position is 0. In each turn, new "O" noughts and "X" crosses are added and the board is filling up. Some of the board settings are indentical up-to-some transformation. As you can see on the picture bellow, both of the boards are equal - the second one is rotated 90° to the left.
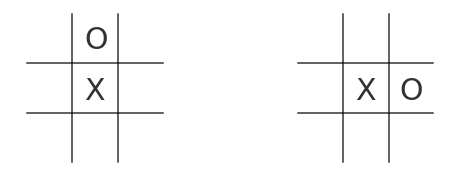
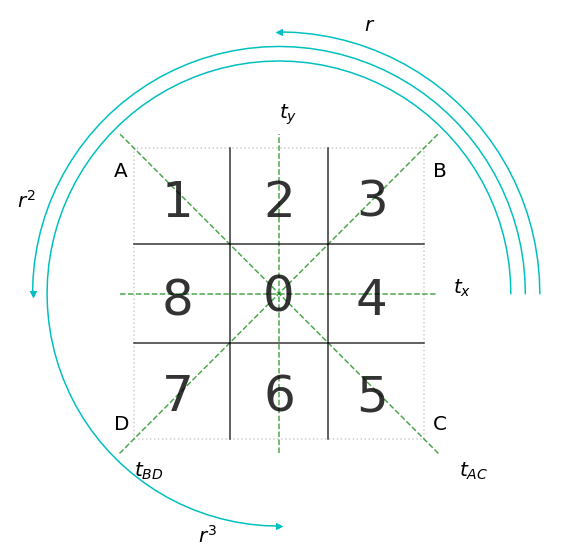
In abstract algebra, we call such operations under which the object is invariant a symmetry group. In the tic-tac-toe case, the underlying shape of the board is a square, therefore, we would be interested in symmetry group of square. Figure bellow shows that we can reflect the square grid about four axes: tx, ty, tAC and tBD, and rotate entire grid about 90° r, 180° r2 and 270° r3, and still get the same square.
This group is called Dihedral Group D4 and it has 8 elements. Generated by ⟨a,b:a4=b2=2,ab=ba−1⟩ For more details see ProofWiki.
Permutations
Each of those group elements {e, r, r2, r3, tx, ty, tAC, tBD} has its own permutation or a mapping for each element projection. For example, an element r rotates the board about 90° to the right, therefore, 0 field maps back to 0, 1 goes to 7, 2->8, 3->1, 4->2, 5->3, 6->4, 7->5, 8->6. However, such notation is a bit confusing we can adopt widely used one - (0, 7, 8, 1, 2, 3, 4, 5, 6), where position or index is the origin and value is the target. In the following table, we can see all the elements' permutations.
Worth noticing that tic-tac-toe permutations do not form the entire permutation group for 8-element set S8. Some permutations would deform the square grid, e.g. applying (1, 2) on the board changes it such that 1 is no longer neighbour with 8, etc. For more details see ProofWiki.
| element | permutation | short cycle form1) |
|---|---|---|
| e | (0, 1, 2, 3, 4, 5, 6, 7, 8) | () |
| r | (0, 7, 8, 1, 2, 3, 4, 5, 6) | (7, 8, 1, 2, 3, 4, 5, 6) |
| r2 | (0, 5, 6, 7, 8, 1, 2, 3, 4) | (5, 6, 7, 8, 1, 2, 3, 4) |
| r3 | (0, 3, 4, 5, 6, 7, 8, 1, 2) | (3, 4, 5, 6, 7, 8, 1, 2) |
| tx | (0, 7, 6, 5, 4, 3, 2, 1, 8) | (1,7) (2, 6) (3, 5) |
| ty | (0, 3, 2, 1, 8, 7, 6, 5, 4) | (1,3) (4, 8) (5, 7) |
| tAC | (0, 1, 8, 7, 6, 5, 4, 3, 2) | (2, 8) (3, 7) (4, 6) |
| tBD | (0, 5, 4, 3, 2, 1, 8, 7, 6) | (1,5) (2, 4) (6, 8) |
As you can see the center field 0 remains fixed for all permutations, which is pretty obvious and gives a clue why we chose 0 as the origin and why the rest of numbers go clockwise all around...
Ternary numbers
If we were interested in the game evolution - how "O" and "X" were added in each turn, we could denote the game as series of cells, e.g. 032 corresponds to 👇
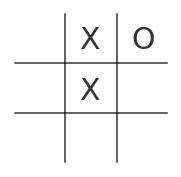
Another handy piece in this tic-tac-toe-algebra puzzle are ternary numbers. All of us are familiar with decimal, hexadecimal and binary numbers, but numbers with base 3 are less common. For the game purposes they suits perfectly as they denote board fields with 0 for empty ones, 1 for "O" and 2 for "X". For example two boards mentioned before, their ternary numbers are 201000000 and 200010000 respectively.
Number of possible boards
Part of a reason why we did all the ☝️ algebra was to came up with number of possible tic-tac-toe boards. We know that the theoretical upper bound of possible games is 9! = 362 880. Factorial takes in count also boards where the game already ended but we added another steps. Henry Bottomley's came up with nice calculations where they estimated 255 168 possible games.
We know that we can do even better by removing all the symmetrical boards, we can count the numbers using some more advance algebra e.g. Burnside's lemma [without any further calculations] can give us better estimate of 2 475 2) or write a fairly short code.
Which give us 765 possible achievable positions where only 138 are possible games regardless on the order of players' moves and transformations.
Putting it all together, we saw that some boards are equivalent up to a symmetry, to find all symmetries for given board we can use the permutations obtained from the symmetry group of square. This observation saved us few thousands boards and we can concentrate on a few classes of boards. For easier notation, we can use handy ternary numbers to denote the boards.
Game theory and minimax theorem
Tic-tac-toe is a perfect information zero-sum game, which means that both players know or at least can find result for all possible moves and when one wins second one lose, and vice versa. From ☝️ computations we know that there are only 765 possible achievable boards which is not that hard to check them all and find the optimal strategy - unbeatable player which can not lose only draw and win.
Computer uses minimax algorithm and plays optimally. If more available options have the same score, it chooses one action at random.
Therefore, we would like to find moves which maximize chances of winning and minimize opponent's chances. In other words - we want to maximize reward and minimize harm in the game. Such an algorithm is called Minimax [6] based on fundamental minimax theorem.
 John von Neumann who proved the Minimax theorem in 1928,
which is considered the starting point of game theory.
John von Neumann who proved the Minimax theorem in 1928,
which is considered the starting point of game theory.
Minimax algorithm
In simulation, when computer player is on turn, it tries to choose actions which have the highest value. We assume that opponent is also a perfect and rational player trying to win and play optimally - the opponent is playing the best available action. Therefore, on opponent's turns we consider the action with the minimum value.
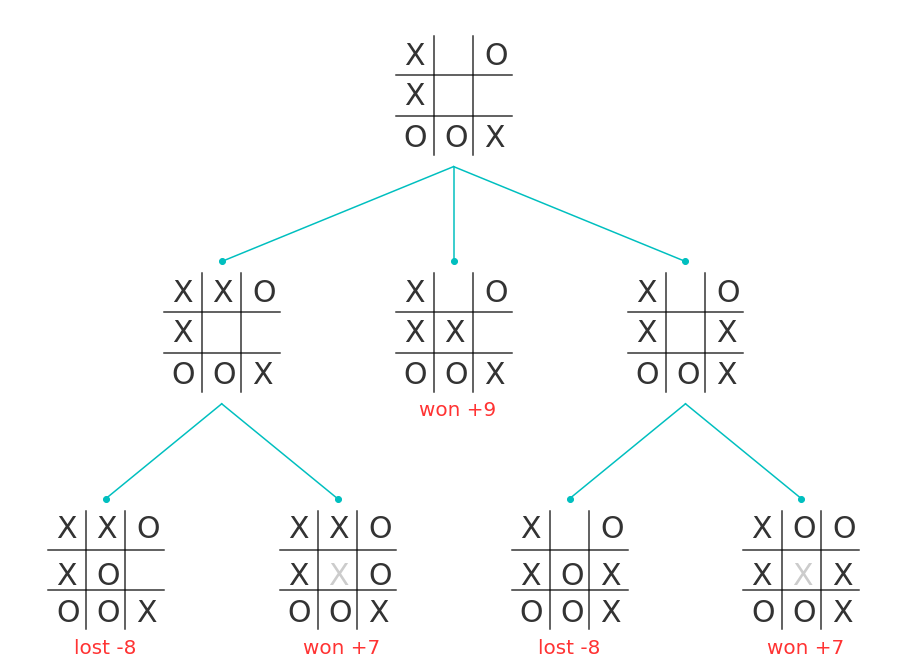 Evolution of all possible boards from "020102112".
Evolution of all possible boards from "020102112".
For every possible action of the board we check what is the value. If computer will win for that action, we assign value "10 - distance between current board and the winning board" or depth. On the other hand, if the action lead to losing the game, we use "depth - 10" as the value. For other scenarios we assign 0.
The figure above shows all possible turns for "020102112" board and value for each path. However, it is "X" turn we are looking for maximum possible value which is "+9". Now we can clearly see that, if player "X" is not playing the "220102112" (middle board) and "O" is perfect player, then "O" tries to maximize its value and plays "12x1x2112". For further analysis check the code bellow.
MENACE or a pile of matchboxes mastering the game
In the times when fast computers were not around, but the concept of computation excited many scientists. British researcher Donald Michie invented very clever idea how to teach matchboxes with colorful beads to play noughts and crosses, which he named "Matchbox Educable Noughts and Crosses Engine" or MENACE.
 The matchbox machine MENACE build by D. Michie [1]
The matchbox machine MENACE build by D. Michie [1]
Each position on the board has its own colour . For every possible board there is a matchbox, bear in mind that we consider only unique symmetry classes. In the first turn matchbox there are initially 4 beads of each possible action represented by the coloured of the beads. For the matchboxes representing third turn, there are 3 beads of each colour, for fifth turns' 2 and for seventh 1. A bead chosen at random decides what action to do at every turn. The opponent turn then define next matchbox and the process is repeated until of the player wins or it is a draw. If the chosen beads led to a winning the game, we add 3 of each color to a corresponding matchbox. If game is a draw, we add 1 extra bead for each matchbox. If MENACE lost the game, we remove the beads.
The fundamental idea of MENACE is to add beads which led to winning and drawing the game, and remove beads which lost the game. Hopping that as more it plays games, the more unbeatable it will be.
If MENACE won the game, we will add three extra beads of winning action to each matchbox representing each turn. For draw we add extra one and if MENACE lost, each of the beads is removed. Following chart demonstrate a dummy version of average reward plot. It demonstrates change in number of beads in the first box. After a few plays you can observe that MENACE is losing every game, after a while it learns not to lose and the reward goes up.
Menace's matchbox brain
Each game below represents one of 304 matchboxes with colourful beads in it. Every available cell denotes number of beads for a give move. Playing the game, beads are added and removed based on the game result in real time.
Reinforcement learning
Like in the MENACE case, the fundamental idea of reinforcement learning is to learn from experience with a carrot and stick method. Where moves which leads to a positive outcome are rewarded with a carrot and negative ones are punished with a stick.
One of the MENACE problems was that it could dies out of memory or some matchboxes lost all beads and MENACE couldn't move forward 3). Learning from MENACE discrete idea we can develop a continues realisation in probability space which will avoid a likely scenario of running out of actions.
Reward and value function
There are some moves which obviously lead to the end of the game and we can assign its final rewards. However, for majority of turns we don't know which tends to win the game and which to lose and draw. Because of that we will distinguish between reward, which gives immediate results and value function which measures the potential of future rewards.
As we are playing, winning and losing, we would like to back propagate rewards from the last moves into the earlier stages of the game. If an agent win the game, we reward it with 1, on the other hand for lost and draw we assigns no point. To do so we define a value function V(·) which assigns potential to every state of board St. In each game we retrospectively update the values using this formula. [3]
The value is derived as a difference between value of previous step (or a reward for final steps) and value of the current step. It is discounted by a learning rate α. Initially, we assign 1s or 0s to all winning and losing states and 0.5 to all others middle-states.
Exploration vs exploitation
If we've played the game purely based on the value function, it is likely that we would stick to play the same all over again. Therefore, we will introduce concept of exploration vs exploitation. In exploration case we pick an action at random regardless on its value. On the other hand, for exploitation we pick the action with highest value. We can alternate those methods at random with ε probability, therefore, we tend to call this method an ε-greedy policy.
Conclusion
"A reason for being interested in games is that they provide a microcosm of intellectual activity in general. Those thought processes which we regard as being specifically human accomplishments—learning from experience, inductive reasoning, argument by analogy, the formation and testing of new hypotheses, and so on — are brought into play even by simple games of mental skill.", said Donald Michie [1]. Games are a specific area of intellectual stimulus which could be computationally solved, such as the example of tic-tac-toe. Therefore, it is worth exploring and playing games using colourful approaches for reaching almost unbeatable perfect player.
Additionally, it is spectacular how a simple game, which every seven years old children learns how to play and not to lose, can attract so much of human interest and different branches of mathematics and computer science.
You can find Python and JavaScript codes for each method in the GitHub repo.
References:
- Michie, D. (1963), "Experiments on the mechanization of game-learning Part I. Characterization of the model and its parameters", Link
- Michie, D. (1961) "Trial and error". Penguin Science Survey.
- Sutton, R. S. & Barto, A. G. (2018), "Reinforcement Learning: An Introduction", The MIT Press.
- Mitchell, M. (2019), "Artificial intelligence a guide for thinking humans", Pelican books
- Scroggs, M. (2015), "MENACE: Machine Educable Noughts And Crosses Engine", Blog post & Game
- Luce, R. D. & Raiffa, H. (1957). "Games and decisions: Introduction and critical survey". New York: Wiley.
- In cycle form we denote only permutations which maps themself in a consecutive chain of elements and leave all elements which maps on themself (fixed points).
-
We can re-frame the lemma to number of possible colorings of a 3x3 grid by three colors, we
get:
$$\frac{1}{|D_4|}\sum_{g\in G}\big |X^g \big| = \frac{1}{8}\bigg( 1\times 3^9 + 3 \times 3^1 + 4 \times 3^3
\bigg)
= 2\ 475$$
(There is one element which leaves all elements unchanged [identity], there are 3 [rotations] which
leave
one element unchanged and 4 [axes] which leave 3 elements unchanged.)
Unfortunately, it says nothing about game possibility - if such board could exists (e.g. all fields are "X"), but it gives us better upper bound. - Actually, there is 1:5 chance that MENACE dies out of beads. One of the possible solution is to add more beads initially; 8 for first turn, 4 for third, 2 for fifth and 1 for seventh.